Webb is a powerful time machine with infrared vision that is peering back over 13.5 billion years to see the first stars and galaxies forming out of the darkness of the early universe.
Early Universe

Out of the Darkness

Webb is able to see back to when the first bright objects (stars and galaxies) were forming in the early universe. Credit: STSci
Why Infrared?
Why is a powerful infrared observatory key to seeing the first stars and galaxies that formed in the universe? Why do we even want to see the first stars and galaxies that formed? One reason is... we haven't yet! The microwave COBE and WMAP satellites saw the heat signature left by the Big Bang about 380,000 years after it occurred. But at that point there were no stars and galaxies. In fact the universe was a pretty dark place.
The Early Universe
After the Big Bang, the universe was like a hot soup of particles (i.e. protons, neutrons, and electrons). When the universe started cooling, the protons and neutrons began combining into ionized atoms of hydrogen (and eventually some helium). These ionized atoms of hydrogen and helium attracted electrons, turning them into neutral atoms - which allowed light to travel freely for the first time, since this light was no longer scattering off free electrons. The universe was no longer opaque! However, it would still be some time (perhaps up to a few hundred million years post-Big Bang!) before the first sources of light would start to form, ending the cosmic dark ages. Exactly what the universe's first light (i.e. stars that fused the existing hydrogen atoms into more helium) looked like, and exactly when these first stars formed is not known. These are some of the questions Webb was designed to help us to answer. See also our Q&A with John Mather about the Big Bang.
Shifted Light
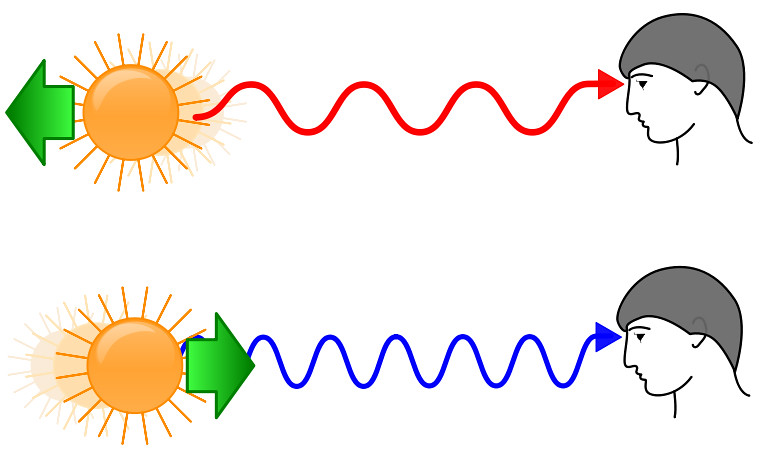
Imagine light leaving the first stars and galaxies nearly 13.6 billion years ago and traveling through space and time to reach our telescopes. We're essentially seeing these objects as they were when the light first left them 13.6 billion years ago. By the time this light reaches us, its color or wavelength has been shifted towards the red, something we call a "redshift." Why? In this particular case, it's because when we talk about very distant objects, Einstein's General Relativity comes into play. It tells us that the expansion of the universe means it is the space between objects that actually stretches, causing objects (galaxies) to move away from each other. Furthermore, any light in that space will also stretch, shifting that light's wavelength to longer wavelengths. This can make distant objects very dim (or invisible) at visible wavelengths of light, because that light reaches us as infrared light.
Webb is able to see back to about 100 million - 250 million years after the Big Bang. But why do we need to see infrared light to understand the early universe? Because light from these objects is shifted to the red. Credit: Aleš Tošovský

Electromagnetic Spectrum Characteristics Credit: NASA
Redshift means that light that is emitted by these first stars and galaxies as visible or ultraviolet light, actually gets shifted to redder wavelengths by the time we see it here and now. For very high redshifts (i.e., the farthest objects from us), that visible light is generally shifted into the near- and mid-infrared part of the electromagnetic spectrum. For that reason, to see the first stars and galaxies, we need a powerful near- and mid-infrared telescope, which is exactly what Webb is!
IN DEPTH
Key Questions
Webb is addressing several key questions to help us unravel the story of the formation of structures in the Universe such as:
- When and how did reionization occur?
- What sources caused reionization?
- What are the first galaxies?
- See also our Q&A with John Mather about the Big Bang.
Webb's Role in Answering These Questions
To find the first galaxies, Webb will make ultra-deep near-infrared surveys of the Universe, and follow up with low-resolution spectroscopy and mid-infrared photometry (the measurement of the intensity of an astronomical object's electromagnetic radiation). To study reionization, high resolution near-infrared spectroscopy is needed.
The Era of Recombination
Until around a few hundred million years or so after the Big Bang, the universe was a very dark place. There were no stars, and there were no galaxies.
After the Big Bang, the universe was like a hot soup of particles (i.e. protons, neutrons, and electrons). When the universe started cooling, the protons and neutrons began combining into ionized atoms of hydrogen and deuterium. Deuterium further fused into helium-4. These ionized atoms of hydrogen and helium attracted electrons turning them into neutral atoms. Ultimately the composition of the universe at this point was 3 times more hydrogen than helium with just trace amounts of other light elements.
This process of particles pairing up is called "Recombination" and it occurred approximately 240,000 to 300,000 years after the Big Bang. The Universe went from being opaque to transparent at this point. Light had formerly been stopped from traveling freely because it would frequently scatter off the free electrons. Now that the free electrons were bound to protons, light was no longer being impeded. "The era of recombination" is the earliest point in our cosmic history to which we can look back with any form of light. This is what we see as the Cosmic Microwave Background today with satellites like the Cosmic Microwave Background Explorer (COBE) and the Wilkinson Microwave Anisotropy Probe (WMAP). Following this are the cosmic dark ages - a period of time after the Universe became transparent but before the first stars formed. When the first stars formed, it ended the dark ages, and started the next epoch in our universe.

Illustration of the Timeline of the Universe. Credit: WMAP
The Epoch of Reionization
Another change occurred after the first stars started to form. Theory predicts that the first stars were 30 to 300 times as massive as our Sun and millions of times as bright, burning for only a few million years before exploding as supernovae. The energetic ultraviolet light from these first stars was capable of splitting hydrogen atoms back into electrons and protons (or ionizing them). This era, from the end of the dark ages to when the universe was around a billion years old, is known as "the epoch of reionization." It refers to the point when most of the neutral hydrogen was reionized by the increasing radiation from the first massive stars. Reionization is an important phenomenon in our universe's history as it presents one of the few means by which we can (indirectly) study these earliest stars. But scientists do not know exactly when the first stars formed and when this reionization process started to occur.

Hubble Deep Field - The first significant look back to the era of the universe when early galaxies were forming. The image is a long exposure of a very small area of the sky, which revealed a large number of very faint, and previously unseen, objects. These objects are some of the oldest and most distant galaxies and allowed us to, as Stefano Cristiani said, "glimpse the first steps of galaxy formation more than 10 billion years ago." Other deeper studies have come after, and Webb will also do deep field studies. Webb's imaging capabilties and infrared vision will show us the early universe with unprecedented clarity. Credit: Robert Williams and the Hubble Deep Field Team (STScI) and NASA
The emergence of these first stars marks the end of the "Dark Ages" in cosmic history, a period characterized by the absence of discrete sources of light. Understanding these first sources is critical, since they greatly influenced the formation of later objects such as galaxies. The first sources of light act as seeds for the later formation of larger objects.
Additionally, the first stars that exploded as supernovae might have collapsed further to form black holes. The black holes started to swallow gas and other stars to become objects known as "mini-quasars," which grew and merged to become the huge black holes now found at the centers of nearly all massive galaxies.



